
















| -3 | -2 | -1 | ml=0 | 1 | 2 | 3 | |
| l=0 |  |
 |
|||||
| l=1 |  |
 |
 |
||||
| l=2 |  |
 |
 |
 |
 |
||
| l=3 |  |
 |
 |
 |
 |
 |
 |
A
spherical harmonic
,
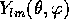 , is a single-valued,
continuous, bounded, complex function of the angular coordinates
, is a single-valued,
continuous, bounded, complex function of the angular coordinates
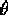 and
and  . They play an important
role in quantum mechanics as the eigenfunctions of the angular momentum
operators
. They play an important
role in quantum mechanics as the eigenfunctions of the angular momentum
operators  and
and 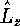 .
Alternatively, the spherical harmonics are a complete basis for the
irreducible representations of the infinite rotations group
.
Alternatively, the spherical harmonics are a complete basis for the
irreducible representations of the infinite rotations group
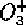 .
.
Depicting the complex functions would require four dimensions. We can represent, however, the real combinations of spherical harmonics defined as:

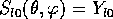
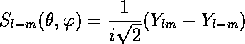
The images have been created using tessel , a program that reads in the analytical expressions that define a parametric surface and produces a quadrilateral or triangular mesh of it. The rendering of the surfaces has been done with POV-Ray 2.2.